study guide: moore, silverman, paoletti, liss, & musgrave 2019

We claim that a person has constructed a convention when that person has in mind a concept, a community of individuals, and some re-presentational practice that he perceives as a choice in that community among a variety of equally valid choices. (p. 181)

Citation

Moore, K. C., Silverman, J., Paoletti, T., Liss, D., & Musgrave, S. (2019). Conventions, habits, and U.S. teachers’ meanings for graphs. The Journal of Mathematical Behavior, 53, 179-195.

https://doi.org/10.1016/j.jmathb.2018.08.002

Inspiration

Gaining insights into the extent students' meanings for relationships and ideas related to function include differentiating between things we (as the researchers) see as convention (i.e., x on the horizontal axis) and things we see as mathematically critical (i.e., constructing a graph that conveys a constant rate of change of 3 between y and x). This empirical study was first motivated by a classroom event. A group of prospective secondary mathematics produced the following two graphs to re-present the relationship between total distance and distance from the ground (i.e., vertical distance) for an individual on an amusement park ride.

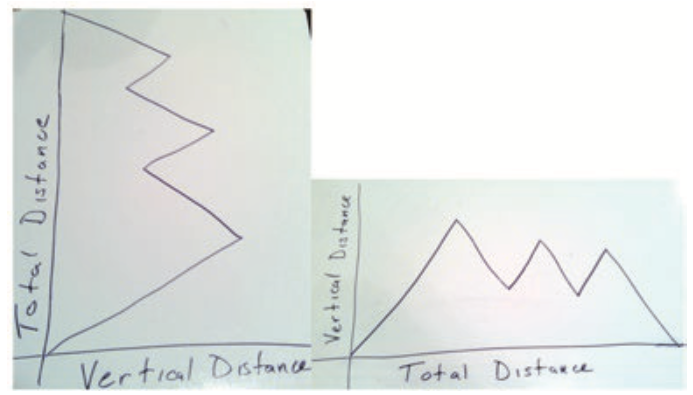
These two graphs were generated by two different groups in the class. As the entire class debated the validity of each graph, they found themselves in an impasse. (1) Each graph re-presented the appropriate relationship between total distance and vertical distance, and thus anything said about the relationship in one graph must be true about the relationship in the other graph. (2) On the other hand, the graph on the right "is a function" and the graph on the left "is not a function." They perceived these two statements to stand in opposition to each other, and as a group they were unable to reconcile the apparent contradiction between these statements after a long, lively debate. As a research group, we grew curious about the meanings driving their actions and assessments of the two graphs. We were particularly curious about the role of "convention" in their meanings and assessments.

Methods and Participants

Semi-structured task-based clinical interviews with 31 undergraduate students in a prospective secondary mathematics teacher program. We also conducted surveys with 45 in-service secondary mathematics teachers.

Takeaway(s)

We inferred three meaning forms. First, we inferred cases in which a participant's meaning was such that it entailed a habitual use of "convention". These were instances in which we inferred that a practice we perceive to be a convention was either maintained apparently unknowingly by the participant or the participant considered the practice to be unquestionably followed, thus not acknowledging other alternatives as viable and correct representations of a mathematical concept. The "convention" was a mathematical rule more privileged that the relationship to be represented. Second, we inferred cases in which a participant's meanings was such that it entailed a convention qua convention. These were instances in which the participant's actions implied her or she understood a practice as a customary, but not necessary, choice in viably (or correctly) representing particular mathematical concepts. The convention was exactly that—a convention—and it was subordinate to the properties of the relationship being re-presented.

A third form of meaning was a particular habitual use of "convention". Termed contradicting actions and claims, these were instances in which the participant's experienced states of perturbation due to their perceiving contradictions or inconsistencies in their meanings. These were also instances in which we perceived contradictory features in their actions and claims but they did not perceive such contradictory features.

To illustrate, I draw attention to this graph.

The participants were first asked whether or not this graph represents a function. After their initial response and interviewer questioning, they were prompted to consider “Is there a way that we (or a student) could consider this graph as representing a function?” After the teacher responded and had indicated he or she exhausted potential responses, the interviewer posed,“What about a student who claims that x is a function of y?"

Of the 25 prospective secondary mathematics teachers given this prompt, all initially claimed the graph did not represent a function. Subsequently, the prospective secondary mathematics teachers had the following response breakdown and example quotes.

Regarding contradicting actions and claims.

...we draw attention to S4 and S14′s responses (Excerpts 3). S4 and S14 claimed the graph as given was not such that x is a function of y, and they claimed the rotated graph was such that x is a function of y. From our perspective, there is a potential contradiction that exists in these two claims: each y-value has a uniquely associated x-value regardless of the orientation of the paper. However, the PSTs’ claims were not a contradiction from their perspective. As we described above, we infer that these PSTs’ meanings for functions and graphs were such that the ways they conceived x–y pairings were dependent on the axes orientations (i.e., habitual use of“convention”), even when presented with prompts and interviewer questions asking them to consider otherwise. (p. 190)

This data illustrates the complexity of responding to what is, on the surface, a rather simplistic prompt. Critically, this data illustrates the subtle role of "convention" or convention qua convention in the participants' meanings, including how it influences the ways in which they assess student work. Those prospective teachers that held meanings consistent with convention qua convention were far more flexible in their assessment of student work, particularly in attributing viable and correct meanings to that student work.

Instructional Implications

As a teacher, ask yourself, "Can my students differentiate between that which is critical to a representation and that which is merely a customary practice?" Alternatively, ask yourself, "Can my students re-present a major idea in conventional and non-conventional ways and see these as mathematically equivalent?" If the answer is no, then there is work to do in supporting their construction of productive and flexible meanings.

Also, consider the evidence you have for a student constructing a productive and flexible meaning for a major mathematical idea. If you stick to conventional representational practices, you are limiting the amount of evidence for or insights into your students' meanings. By giving them opportunities to construct representations that both follow and do not follow conventions, you gain deeper insights into the properties your students perceive as critical to re-presenting some mathematical idea.

As a teacher, ask yourself, "Did my students have an opportunity to negotiate and establish a convention?" If the answer is no, then it is likely the case that what you perceive to be a convention is instead perceived by your students to be a mathematical fact or rule. Give your students opportunities to engage in different representational practices, realize the annoyance of doing so, and negotiate a common practice among them and their peers in the class. Remember, a person has constructed a convention when that person has in mind a concept, a community of individuals, and some re-presentational practice that he perceives as a choice in that community among a variety of equally valid choices.

Oh, one last thing. It is a bit sloppy to state "a graph is/is not a function," especially if the community of learners have not explicitly established what is meant by "a graph". It is more mathematically precise to speak to "x is/is not a function of y", "y is/is not a function of x", "vertical distance is a function of total distance", etc.